Les Annales de Gergonne: un bicentenaire
2010 marque le bicentenaire de la publication du premier grand journal de l'histoire des mathématiques: les Annales de mathématiques pures et appliquées (1810-1832) de Josep-Diez Gergonne (1771-1859)
Christian Gérini
Le bicentenaire de la publication du premier grand journal de l'histoire des mathématiques: les Annales de mathématiques pures et appliquées (1810-1832) de Josep-Diez Gergonne (1771-1859)
Depuis mon travail avec Alain Michel sur les Annales de Gergonne, j’ai été conduit à m’intéresser à l’évolution des journaux consacrés uniquement aux mathématiques parus en France entre 1810 et 1850. Norbert Verdier m’a éclairé sur le Journal de Liouville, et nous avons mené ensemble quelques études comparatives entre ces deux périodiques. Le LPHS de Nancy m’a fait « entrer » dans les Nouvelles Annales et m’a permis de compléter ma vision des mathématiques et des formes – et contenus - de leur diffusion périodique durant la deuxième moitié du 19ème siècle.
Ces différents travaux m’ont conduit à certaines conclusions que je vais tenter de relier à une chronologie et au peu que je sais des journaux savants du 18ème siècle, et plus particulièrement du Journal des savants cher à Jeanne Peiffer et à Jean Pierre Vittu.
Je précise que, contrairement à Norbert Verdier sur le Journal de Liouville, je ne me suis pas intéressé à propos de Gergonne à la question de ses libraires imprimeurs et des problèmes de typographie, ni à son lectorat : mon premier travail ayant consisté en une thèse en philosophie et histoire des mathématiques, j’ai plutôt persévéré dans cette voie, privilégiant les contenus, les croisements de disciplines, les champs disciplinaires affichés, et la nature (fonctions, origine) des auteurs.
LES ANNALES DE GERGONNE.
Le journal d’un homme à tout faire.
J.D. Gergonne, et Thomas Lavernède, les deux rédacteurs des Annales au début de leur parution (c'est-à-dire les deux premières années) sont professeurs de mathématiques au lycée de Nîmes. On peut donc considérer que ce journal est la volonté de deux « spécialistes », si tant est que ce terme soit bien défini à l’époque. En fait, la lecture du « Prospectus » d’introduction paru dans le premier numéro en juin 1810 et des commentaires et notes dans le journal lui-même, montre rapidement que Gergonne est l’auteur de tous les textes annexés aux articles, et le seul vrai rédacteur de la revue. La lecture de tous ses écrits, publiés ou manuscrits (dont quelques centaines de lettres que j’ai consultées au Caran, aux AD et AM de l’Hérault et du Gard, etc.), permet de ne pas douter de ce point : sa « griffe » est facilement reconnaissable, et l’on pourrait même s’ « amuser » à en reconnaître l’influence et la trace dans les écrits de ses auteurs. Je ne vais donc à présent ne parler que de Gergonne comme LE rédacteur de ses Annales.
C’est d’ailleurs lui qui, durant les 22 ans de parution des Annales, recevra les manuscrits de ses auteurs, les publiera en se permettant parfois de les corriger et souvent de les annoter. On a perdu la plupart de ces envois, mais il en reste quelques uns aux archives de la faculté des sciences de Montpellier. Gergonne est donc à lui seul le « comité de rédaction » de son journal (peut-être aidé par Thomas Lavernède de 1810 à 1812, mais rien ne permet pour l’instant de le confirmer).
En outre, on a retrouvé une partie des planches gravées de géométrie (publiées en fin de chaque volume annuel) dans les affaires de Gergonne : il les gravait lui-même sur cuivre, les signant de sa main.
Gergonne est-il un « spécialiste » des mathématiques ? Quelles sont ses motivations ? Comment constitue-t-il ses réseaux d’auteurs ? Comment parvient-il à être « reconnu » aussi rapidement, alors qu’il publie depuis une province éloignée de Paris ? Ce sont les premières questions que l’on se pose.
Ses Annales sont-elles un journal de mathématiques spécialisé? La réponse à cette question est plus délicate, comme je vais le montrer. Et pour tenter de la trouver, nous nous apercevrons qu’il faut sortir des mathématiques, et se méfier de toute vision rétrospective.
Avant de s’intéresser à ces questions, il faut tenter de définir ce qu’on entend par «mathématiques » en 1810. Ce qui mène à se poser aussi la question que Jeanne Pieffer s’est elle-même posée à propos du Journal des savants : qu’est-ce qu’un géomètre ? Et de répondre en même temps à la question de la motivation des deux rédacteurs aux origines de leur journal.
En effet, le début du Prospectus d’introduction nous indique la motivation première, et en même temps nous parle de « géomètres « et de « sciences exactes » sans mentionner encore le mot «mathématiques » :
«C'est une singularité assez digne de remarquer que, tandis qu'il existe une multitude de journaux relatifs à la Politique, à la Jurisprudence, à l'Agriculture, au Commerce, aux Science physiques et naturelles, aux Lettres et aux Arts; les Sciences exactes, cultivées aujourd'hui si universellement et avec tant de succès, ne comptent pas encore un seul recueil périodique qui leur soit spécialement consacré(**), un recueil qui permette aux Géomètres d'établir entre eux un commerce ou, pour mieux dire, une sorte de communauté de vues et d'idées; un recueil qui leur épargne les recherches dans lesquelles ils ne s'engagent que trop souvent en pure perte, faute de savoir que déjà elles ont été entreprises; un recueil qui garantisse à chacun la priorité des résultats nouveaux auxquels il parvient; un recueil enfin qui assure aux travaux de tous une publicité non moins honorable pour eux qu'utile au progrès de la sciences. »
I. L’ambition est clairement affichée :
Etablir une « émulation » (un « commerce d’idées ») au sein d’une « communauté » qui se reconnaîtrait et se ferait reconnaître, éviter des recherches inutiles, et assurer la promotion de travaux utiles « au progrès de la science ».
Le succès de l’entreprise, comme l’intérêt que suscitent encore aujourd’hui les Annales, seront révélateurs a posteriori de la pertinence de ces objectifs.
Emulation, promotion, communauté. Je m’arrête un instant sur ces trois termes.
L’émulation sera effective, comme je l’ai montré dans le chapitre sur les controverses de ma thèse, ou dans des débats qui entourèrent les articles de calcul différentiel, de géométrie des imaginaires, ou de géométrie projective, dont j’ai parlé par ailleurs. Gergonne insiste d’ailleurs sur ce point dans le même document : « Chaque numéro des Annales offrira un ou plusieurs Théorèmes à démontrer, un ou plusieurs problèmes à résoudre. Les Rédacteurs, dans le choix de ces théorèmes et problèmes, donneront la préférence aux énoncés qui pourront leur être indiqués par leurs correspondans; et ils consigneront, dans leur recueil, les démonstrations et solutions qui leur seront parvenues; ils espèrent ainsi provoquer chez les jeunes géomètres une utile et louable émulation. Personne n'ignore d'ailleurs combien ces sortes de défis ont ajouté de perfectionnement à l'analise, au commencement du dernier siècle ; et il n’est point déraisonnable de penser qu'en les renouvelant, on peut, peut-être, lui préparer encore de nouveaux progrès. ». L’émulation et les controverses s’exerceront bien au-delà des simples défis que représentaient les théorèmes non démontrés.
La « promotion» des travaux des mathématiciens ainsi visés se fera de deux façons différentes :
1- la première, déjà largement pratiquée dans les journaux savants des siècles précédents (le Journal des savans, The Mathematical Repository, les Philosophical Transactions etc.) consistera en des comptes-rendus d’ouvrages. Gergonne écrit à ce propos dans son Prospectus : « Enfin, un objet auquel on se propose de donner, dans ces Annales, une attention toute particulière, à raison de l'extrême utilité que le public peut en retirer, c’est l'annonce et l'analise des ouvrages nouveaux, tant nationaux qu'étrangers, relatifs aux sciences mathématiques et aux autres sciences qui en dépendent. ». Il restera fidèle à cette intention jusqu’au dernier numéro en 1832. Et la publicité qu’il fera par exemple au Journal de Crelle conduira à de fructueux échanges d’articles entre les deux personnages.
2- La publication des articles s’inscrivant dans la ligne éditoriale, quels qu’en soient les auteurs, et sans censure de classe ou de champ disciplinaire. On trouvera en effet tout au long des 22 années de publication des contributions d’élèves de collèges comme de membres d’académies ou de professeurs de facultés ou de grandes écoles, français ou étrangers, et la diversité des rubriques dont je reparlerai plus loin vient confirmer l’esprit d’ouverture qui animait les rédacteurs.
La « communauté » est donc très large. Gergonne exprime une frustration liée à son éloignement de la capitale et de ses élites : « Les Rédacteurs des Annales sentent fort bien tout ce que la distance où ils se trouvent du centre des lumières peut ajouter de difficultés à leur entreprise; mais, plus jaloux de leur réputation et de l'estime des savans que soigneux de leurs intérêts pécuniaires, ils sont résolus de faire tomber sur eux seuls tous les sacrifices auxquels la position peu commode où ils se trouvent doit inévitablement les exposer ». Il avoue son échec à convaincre les mêmes élites à fonder (avec lui) un tel journal : « Ils (les rédacteurs) avaient même fait, auprès de quelques personnes plus à portée et mieux en état qu'eux de l'exécuter, les démarches pressantes pour les solliciter à l'entreprendre; et le non succès de ces démarches a seul pu les enhardir à s'en charger eux-mêmes ». Et il veut intéresser ces élites : « Ils (les rédacteurs) osent croire (…) que les savans même qui pourraient le mieux se passer des secours qu'un ouvrage de la nature de celui-ci est susceptible d'offrir, ne dédaigneront pas néanmoins d'accorder leur encouragement honorable à une entreprise dont le succès ne peut que contribuer encore à l'avancement de ces mêmes sciences ». Mario Otero et Jean Dhombres y ont vu la volonté d’un homme de donner la parole aux « oubliés », à une « communauté enseignante » isolée dans ses établissements de province. L’insistance que Gergonne mettra pour obtenir le titre de correspondant de l’académie, ses engagements politiques avant et pendant sa carrière rectorale, ses courriers innombrables aux ministres, nous font plutôt penser à une volonté de se hisser à la hauteur de ces mêmes élites. Mais le résultat n’en est pas moins là. Si nous ne disposons pas de registres des abonnés, la population d’auteurs nous renseigne cependant sur la double réussite de son entreprise : la communauté enseignante dans son ensemble est représentée, et les mathématiciens de renom finiront par adhérer à son journal en y publiant des articles entre 1820 et 1830, comme l’a noté Amy Dahan.
Là encore, cette dernière remarque est à relativiser : les contributions de ces élites dans la dernière décennie de parution des Annales sont numériquement bien moindres que celles qu’elles publient par exemple dans le Bulletin de Ferrussac, voire dans la Correspondance de Quételet, qui n’étaient pourtant pas uniquement consacrés aux mathématiques.
II. La définition du mot « mathématiques » et la question de la spécialisation.
Ce qui nous amène à revenir sur la question de la définition du mot « mathématiques » au début du 19ème siècle. Et à nous demander si Gergonne était un « spécialiste », de même que ses lecteurs et auteurs.
Mathématiques ou sciences exactes ? Mathématiciens ou géomètres ?
Les Annales de Gergonne furent le premier grand périodique du 19ème siècle consacré uniquement aux mathématiques, et nul ne doute que son contenu se rapporte essentiellement à ce que nous nommons aujourd'hui ainsi.
Cependant, le terme de géomètre est souvent préféré à celui de mathématicien. Certes, nous sommes au début du XIX° siècle, mais l'héritage classique pèse encore, y compris dans les dénominations, et en particulier dans ce cas: l'éternel géomètre" de Platon, le rang de "grand géomètre" attribué à Apollonius, et celui plus modeste de "géomètres" donné aux arpenteurs des rives du Nil, sont les exemples traditionnels que Gergonne reprend lui-même dans un article sur la synonymie mathématique (T. 8, 1817-1818, p. 156).

Gergonne nous renseigne à la fois sur la persistance de l’emploi du terme de « géomètres », et sur sa propre vision des mathématiques, les seules « sciences exactes » à ses yeux. Finalement, les géomètres s’occupent de bien d’autres choses que de géométrie (nous le verrons évidemment dans toutes les rubriques représentées), mais travaillent dans des domaines relevant de l’exactitude des raisonnements et des calculs, au sens de la logique déductive héritée d’Aristote et de Port Royal (et que Gergonne enrichit dans un long article de « dialectique rationnelle » au T.7, 1816-1817, p. 189-228 ), domaines qui seuls peuvent se retrouver sous l’appellation de « mathématiques » au sens où il l’entend.
Cet élargissement du champ de la seule « géométrie » à celui de la mathématique telle que nous la voyons aujourd’hui a été évidemment noté bien avant cette époque. Jeanne Peiffer et Jean Pierre Vittu nous parlent bien d’un thème « souvent abordé » dans le Journal des savants, l’ « introduction du calcul algébrique dans les démonstrations de géométrie ».
Le débat est toujours d’actualité au début du 19ème siècle, et on le retrouve dans les Annales par exemple en 1817, T. 8, p. 141-152, dans un article de Poncelet que Gergonne classé en « philosophie mathématique » (ce qui est déjà signifiant en soi), et auquel il répond sous forme très polémique (T. 8, p. 156-161): « Réflexions sur l’usage de l’analyse algébrique dans la géométrie, suivies de la solution de quelques problèmes dépendant de la géométrie de la règle ».
Là encore, le Prospectus permet d’apprécier les démarcations faites par le rédacteur entre « mathématiques pures », « sciences exactes » et applications :
« Ces Annales seront principalement consacrées aux Mathématiques pures, et surtout aux recherches qui auront pour objet d'en perfectionner et d'en simplifier l'enseignement. Le titre de l'ouvrage annonce assez d'ailleurs que, si l'on n'y doit rien rencontrer d'absolument étranger au Calcul, à la Géométrie et à la Méchanique rationnelle, les rédacteurs sont néanmoins dans l'intention de n'en rien exclure de ce qui pourra donner lieu à des applications de ces diverses branches des sciences exactes. »
%
La dernière précaution permettra d’élargir le champ des mathématiques appliquées par exemple à des questions d’arithmétique politique, offrant ainsi une tribune au polémiste Gergonne… Mais à de rares exceptions près, la seule discipline classée dans ces mathématiques appliquées que nous ne trouverons plus dans les revues ultérieures est celle de « philosophie mathématique » que Gergonne n’annonce d’ailleurs pas dans son Prospectus (je vais y revenir) :
« Ainsi, sous ce rapport, l'Art de conjecturer, l'Economie politique, l'Art militaire, la Physique générale , l'Optique, l'Acoustique, l'Astronomie, la Géographie, la Chronologie, la Chimie, la Minéralogie, la Météorologie, l'Architecture civile, la Fortification, l'Art nautique et les Arts mécaniques, enfin, pourront y trouver accès. On aura soin, au surplus, de consulter, à cet égard, le vœu du plus grand nombre des souscripteurs, et de s'y conformer scrupuleusement. »
Un document de référence, et concomitant à l’apparition des Annales (puisque publié en 1810, bien que remis à l’Empereur en 1808) permet de situer les disciplines admises par Gergonne par rapport à ce que l’on entendait officiellement par « mathématiques » à l’Institut : il s’agit du Rapport à l’Empereur sur le progrès des sciences, des lettres et des arts depuis 1789, de Jean-Baptiste Delambre, et plus particulièrement de sa section I (mathématiques).
Proportions des champs mathématiques du rapport Delambre (1808) (Source: Jean Dhombres, introduction à la réédition de 1989):
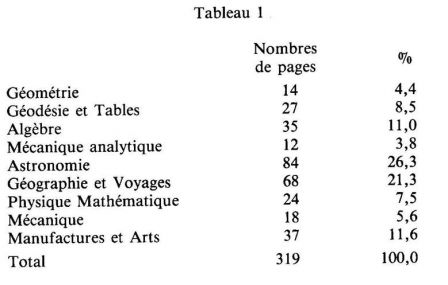
Proportions des champs mathématiques dans les mémoires de la première classe de l’Institut avant 1808 (Source: Jean Dhombres, introduction à la réédition de 1989 du rapport Delambre):

Finalement, les Annales de Gergonne sont bien un journal uniquement consacré aux mathématiques et à leurs applications, si l’on prend ces dernières en un sens assez large partagé à l’époque. Le souci premier des éditeurs (les « recherches qui auront pour objet d'en perfectionner et d'en simplifier l'enseignement ») sera en revanche largement contredit : un nombre important d’articles sont inaccessibles au commun des élèves ou des professeurs de l’époque, et exposent simplement le fruit de recherches et d’avancées en dehors du contexte scolaire, ou du moins à un niveau où la recherche et les découvertes ont autant leur importance que la présentation didactique (école polytechnique, facultés, académies nationales).
Publié le lundi 12 avril 2010 par Christian Gérini